The Hurst Tournament Mean System (HTM)
by Tom Hurst
Introduction
There has been much talk of late concerning what is the best possible rating system for
tournament Diplomacy. Not being one to keep from putting in him two cent’s worth when
everybody else is, I’ve decided to pass on a little system that I devised one night
while in em alcoholic stupor which, for lack of a better name, I choose to call the Hurst
Tournament Mean system, or HTM for short.
The basic premise behind the HTM system is the realization that no rating system is
adequate to compare the wide range of Diplomacy games played. Between different games
played in different ways (email, postal, FtF) there are great differences just in the way
the diplomacy is conducted, if in nothing else. I do not believe that any sensible
comparison can be made. Games should be played under similar conditions in order to be
ranked in a similar fashion. Since the most important need at the moment is for a rating
system that will allow a tournament director to rank the players in that tournament for
the purpose of distributing prizes and titles, I have decided to concentrate solely on
that. At least, one can assume for working purposes that all the games played in any given
tournament will be played in a similar setting. Thus, the HTM system is designed solely
for tournaments.
Another thing that a ranking system should address is the suggestion of what it is
really trying to measure. Although others will perhaps debate the point, I believe that a
ranking system should measure how a player does in relation to what all the other players
do, given the ease playing conditions and country. It would be nonsense to assume that a
player who plays Italy can grow as fast as one playing France in the first few rounds of a
given game, just to give an example. This does not mean that either country’s overall
chances of ultimately winning a game are greater or lesser - it is just that the playing
styles for each country perforce differ. Thus to compare the absolute scores of France and
Italy after an arbitrary number of rounds without playing a game to its conclusion -
something rarely seen in tournaments - would be akin to comparing apples to oranges. What
the HTM system does is to compare the Italians to the other Italians in the tournament.
The ultimate winner of the tournament will be he who does the best of all the players in
similar conditions.
A third item that should be considered is the question of meta-gaming. Let’s face
it. Meta-gaming in tournaments is a fact of life, no matter how much we deplore the
practice. It is foolish to assume that we can snap our fingers and make it go away.
However the ranking system in a tournament should take this into account, making it as
difficult as possible to meta-game. The HTM system makes it impossible to determine a
player’s final more until after the last game of the last round of the tournament is
over. Until that time, a player can ascertain his and others approximate score if he
wishes to and can afford to take the time to do so, but he won’t know for sure what
anyone’s final score will be until the tournament is over.
With these things in mind, let us look at the rules of the HTM system and then apply
these rules to a small tournament to see how they work.
THE RULES
1. A tournament in which this system is used must contain enough games for the average
final score for each country to be representative. It is suggested that the tournament
consist of at least three rounds or ten games at a minimum.
2. No player can play the same country twice in the same tournament unless he has
played each country at least once.
3. At the conclusion of each game (using whatever tournament rules are applicable), the
number of supply centres controlled by each player is recorded and given to the Tournament
Director.
4. If a player is eliminated, his supply centre score for that game is zero. If he is
not eliminated, his score is the number of SC’s he controls at the end of play.
5. The average (mean) score for the tournament of the country a player played is
subtracted from his SC score for the game he played that country to yield that
player’s finished country score.
6. The sum of all adjusted country scores for a player is divided by the number of
rounds played to yield the player’s final score.
7. For those mathematically inclined, the formula for calculating a player’s final
score is…
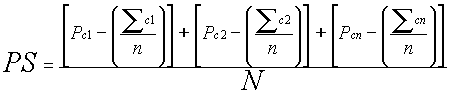
Where:
| PS |
= |
Player’s score |
| Pc1 |
= |
Player’s SC score in the first round |
| Pc2 |
= |
Player’s SC score in the second round |
| Pcn |
= |
Player’s SC score in the nth round |
 |
= |
The sum of all the SC scores for the whole tournament of the
country that the player played in the first round |
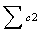 |
= |
The sum of all the SC scores for the whole tournament of the
country that the player played in the second round |
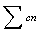 |
= |
The sum of all the SC scores for the whole tournament of the
country that the player played in the nth round |
| n |
= |
The number of games played in the tournament |
| N |
= |
The number of rounds played in the tournament |
8. All scores will be rounded to four decimals or further if ties need to be broken.
(In other words, get yourselves a calculator!)
An Example Of The System At Work
Assume a 21 player tournament. Players are identified by P1, P2, P3… P21.
Countries played are identified by the letter. Scores are identified by number.
Round 1 Results
| Game 1 |
Game 2 |
Game 3 |
| P1 - A – 6 |
P8 - A – 10 |
P15 - A – 6 |
| P2 - E – 5 |
P9 - E – 0 |
P16 - E – 6 |
| P3 - F – 10 |
P10 - F – 8 |
P17 - F – 0 |
| P4 - G – 0 |
P11 - G – 6 |
P18 - G – 5 |
| P5 - I – 8 |
P12 - I – 5 |
P19 - I – 0 |
| P6 - R – 6 |
P13 - R – 0 |
P20 - R – 10 |
| P7 - T - 0 |
P14 - T - 6 |
P21 - T – 8 |
Let us follow one player P1. His SC score for round one was 6 playing as Austria.
Let’s see how this plugs into the formula:

| Pc1 |
= |
Player’s SC score in the first round |
= 6 |
 |
= |
The sum of all the SC scores for the whole tournament of the
country that the player played in the first round |
= 22 |
| n |
= |
The number of games played in the tournament |
= 3 |
| N |
= |
The number of rounds played in the tournament |
= 1 |

Thus Player 1 has a score of –1.3333 as at the end of the first round.
Round 2 Results
| Game 4 |
Game 5 |
Game 6 |
| P19 - A – 0 |
P20 - A – 5 |
P21 - A – 0 |
| P16 - E – 6 |
P17 - E – 0 |
P18 - E – 10 |
| P13 - F – 10 |
P14 - F – 8 |
P15 - F – 6 |
| P10 - G – 5 |
P11 - G – 6 |
P12 - G – 6 |
| P7 - I – 6 |
P8 - I – 10 |
P9 - I – 8 |
| P4 - R – 0 |
P5 - R – 0 |
P6 - R – 0 |
| P1 - T - 8 |
P2 - T - 6 |
P3 - T – 5 |
This time Player 1 played Turkey where he scored 8. Taking into account this score and
his score of 6 as Austria the previous round we extend the formula as follows:

| Pc1 |
= |
Player’s SC score in the first round |
= 6 |
| Pc2 |
= |
Player’s SC score in the second round |
= 8 |
 |
= |
The sum of all the SC scores for the whole tournament of the
country that the player played in the first round |
= (6+10+6+0+5+0) = 27 |
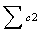 |
= |
The sum of all the SC scores for the whole tournament of the
country that the player played in the second round |
(0+6+8+8+6+5) = 33 |
| n |
= |
The number of games played in the tournament |
= 6 |
| N |
= |
The number of rounds played in the tournament |
= 2 |

Therefore after two rounds Player 1’s score has risen to 2.0000. Remember that a
new average score for each country played is calculated after each round. Here the
Austrian average score changed from 7.3333 to 4.5000 from the first to the second round
because of the poor Austrian showing in round 2. The situation could just as easily have
been the other way around. If this doesn’t stop meta-gaming, I don’t know what
will!
Reprinted from The Flying Dutchman No.9 (April 1980)
| 



