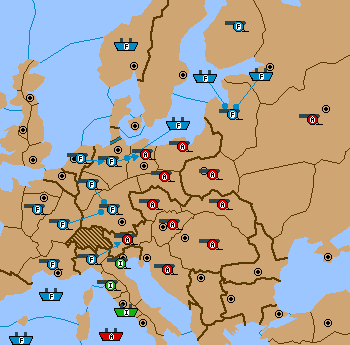
All of this is quite interesting. But in point of fact, we don't really need to analyze the French Berlin position to evaluate the French Munich position. Does this surprise you?
FA is certainly one of the crucial sets of orders for France. And, we may comfortably conclude, AC is one of the crucial sets of orders for Austria. For consider. There is really no other set of orders for Austria that can counter FA. (There are minor variants on AC, of course, but we will treat those as the "same move" as AC.) Straying in any significant way from AC will leave Austria in a very bad position if France does order FA. (A student asks: "What about the move fragment, Ber-Mun, Sil S Ber-Mun, Boh S Ber-Mun?" This I am considering a "minor variant" of AC. The only reason I get to count it that way is that it does not give results different from AC's in any relevant combination of French and Austrian moves. Good question, though. Please verify my claim for yourselves.)
A good general plodding sort of attack on endgame problems is this. Find a plausible move for one side. (If there is an obvious "attacking" side and "defending" side, look for the good attack first.) Find the best countermove for the other side. Then see whether there's an obvious, all-around plausible move for the first side that trounces the countermove. That's what we'll do now. We want to find a move for France that will outright win against AC.
Now, there are many of these. AC is a very risky move. If France could just hold Munich, by supporting it in place, and still have his double attack on Berlin, using Baltic and Kiel, he would have his 18 centers. ("But what if it's a Spring move?" That doesn't matter here. Once taken, Berlin and Munich will be easy for France to hold. Really, are you sure you belong in this class?) Does it matter which one we choose? A bit, yes. Since we have some choice in the matter, let's think for a moment about what other desiderata there are.
Many seasoned endgame analysts, no doubt including many of you, will always try to find the treasured "Safe Move." A Safe Move cannot lose ground against any opposing move. A really good Safe Move should itself make some progress under some (plausible) circumstances. And France, to her delight, has one of these. And it is one of the moves that wins instantly against AC. So let's give her that move now. At a loss for any creativity at the moment, we shall call it
French Safety:
A Mun H, A Lvn H, A Kie-Ber, F Bal S Kie-Ber, F StP S A Lvn, F GoB S A Lvn, F Nwy H, A Fin H, A Hol - Kie, A Bur S A Mun, A Ruh S A Mun, A Par H, A Pie - Tyo.

Two of the Austrian armies bordering Munich are attacked by armies other than A Mun, and Mun is twice supported. A Lvn is twice supported. No French unit can be dislodged. So 'French Safety' is properly named. But against AC, French Safety (ok, let's call it FS) wins immediately. For the resulting position holds Berlin and Munich, thus 18 centers, indefinitely, against any Austrian attack.
We now know of two French moves and one Austrian move. FS wins against AC. FA leads to a yet-unevaluated position against AC. France seems to have so far no reason to play anything but FS. If we can give him no reason, the position is very dull. Can we? Sure. FS clearly does not force a win. Austria has a perfectly good reply, in fact, many. He has to defend Berlin adequately; then there is no change in position after the move. If Austria could actually make progress, dislodging A Lvn or even taking Munich, the move that would do it would be a critical one. But there is no such move. As we noted, "French Safety" is correctly named. So we need to find an Austrian move that leaves the position unchanged when played against FS. These are a dime a dozen. I leave their discovery as an exercise. Pick your favorite, call it AD (for Austria Defends).
Now we have two moves apiece. Let's chart the results of interactions between pairs of moves in a little matrix.
| AD | AC | |
| FS | - | w |
| FA | w | ? |
The entries in the four cells in the table evaluate the results of pairing the moves in question. The "w" stands for French Win. The dash means No Change. The question mark is there because we have not evaluated the French Berlin position. Now, you might expect that we couldn't evaluate the initial position at all until we can evaluate French Berlin; but as I said, that's wrong. We don't have to evaluate French Berlin. The position is a virtually forced win for France. How do we know?
To simplify, assume the worst for France. Assume that French Berlin is an absolutely drawn position. (It isn't). Even in this worst case, France is sitting pretty.
 Now stop for a
moment and figure out why. You needn't look at the map at all, just look at
the matrix.
Click here when your pencil is back on your desk.
Now stop for a
moment and figure out why. You needn't look at the map at all, just look at
the matrix.
Click here when your pencil is back on your desk.